Bội Số Là Gì ? Ứng Dụng Của Bội Số Bội Số Là Gì

Tìm bội số hoặc ước số là một dạng toán hết sức cơ bản của lớp 6 nói riêng và của Trung học cơ sở nói chung. Tuy nhiên, khi học quá nhiều môn và thu nhận quá nhiều kiến thức khiến các bạn dễ dàng quên mất bội số là gì, ước số là gì và áp dụng vào bài toán như thế nào. Bài viết sau đây sẽ giúp các bạn củng cố kiến thức về bội số là gì, ước số là gì và những dạng toán liên quan nhé!

Bội số là gì? Cách tìm bội số chung nhỏ nhất?

Bội số là gì?

Trong toán học chúng ta thường được nhắc đến từ bội số. Tuy nhiên cũng khá nhiều bạn thắc mắc không hiểu rõ về nghĩa của bội số là gì ? Có thể tính bội số như thế nào? 

Toán học là bộ môn quan trọng trong chương trình giáo dục nước ta, nó có tính ứng dụng thực tế cao. Kiến thức về bộ toán học này rất đa dạng, phong phú nên nhiều bạn học không thể nắm bắt hết được.

Đang xem: Bội số là gì

Bước vào lớp 6 thì các bạn học sinh đã bắt đầu được làm quen với môn đại số, trong đó, kiến thức về bội số, ước số là những cái mà các em sẽ phải tiếp xúc và quen. Kiến thức về bội số chúng ta cũng đã học rất nhiều, có thể một số bạn học lại không nhớ rõ. Kiến thức này được ứng dụng trong rất nhiều bài tập, bài thi nên bạn học phải chú ý để có thể giải đáp một cách chính xác nhất.

Trong tiếng Anh bội số được viết là multiple.

Bội số của A là các số chia hết cho A. Bội số nhỏ nhất của A là số nhỏ nhất chia hết cho A.

Ví dụ: Bội số của 3 là các số 3, 6, 9, 12, 15,…

Bội số nhỏ nhất của 3 là chính nó.

Bội số của A là các số chia hết cho A

Bội số chung nhỏ nhất là gì?

Bội số chung nhỏ nhất được hiểu là số nhỏ nhất khác 0 có thể chia hết cho 2 hoặc nhiều số tự nhiên khác nhau. Nếu a và b bằng 0 thì không tồn tại số nguyên dương chia hết cho a, b, khi đó bội số chung nhỏ nhất được quy ước bằng 0.

Ví dụ: Bội số chung của 2 và 3 là tập hợp những số tự nhiên khác 0 chia hết cho cả 2 và 3. Theo đó, chúng ta có thể dễ dàng tìm được 6 chính là số nhỏ nhất chia hết cho cả 2 và 3. Vậy có thể nói, 6 là bội số chung nhỏ nhất của 2 và 3.

Ước số là gì?

Số nguyên dương b lớn nhất là ước của cả hai số nguyên a, b được gọi là ước số chung lớn nhất (ƯCLN) của a và b. Trong trường hợp cả hai số nguyên a và b đều bằng 0 thì chúng không có ƯCLN vì khi đó mọi số tự nhiên khác không đều là ước chung của a và b.

Nói theo cách khác ước số là một số tự nhiên khi một số tự nhiên khác chia với nó sẽ được chia hết.

Mô tả rõ hơn thì khi một số tự nhiên A được gọi là ước số của số tự nhiên B nếu B chia hết cho A.

Ví dụ: 6 chia hết được cho <1,2,3,6>, thì <1,2,3,6> được gọi là ước số của 6.

Kí hiệu :

B(a) : tập hợp các bội của a.

Ư(a) : tập hợp các ước của a.

Ước chung lớn nhất là gì?

Ước số chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp ước chung.

Một số dạng toán về UCLN và BCNN

Từ các định nghĩa ước chung lớn nhất là gì hay thế nào là bội chung nhỏ nhất, dưới đây là một số bài tập về ước và bội điển hình và cơ bản.

Ví dụ 1: Tìm ƯCLN của:

a) 40 và 60b) 24, 84, 180

Cách giải

a) 40 và 60

Ta có: (40=2^{3}.5); (60=2^{2}.3.5)

Vậy (UCLN(40,60)=2^{2}.5=20)

b) 24,84,180

Ta có: (24=2^{3}.3); (84=2^{2}.3.7); (180=2^{2}.3^{2}.5)

Vậy (UCLN(24,84,180)=2^{2}.3=12)

Ví dụ 2: Tìm BCNN của:

a) 84 và 108b) 24, 40, 168

Cách giải

a) 84 và 108

Ta có: (84=2^{2}.3.7); (108=2^{2}.3^{3})

Vậy (BCNN(84,108)=2^{2}.3^{3}.7=756)

d) 24, 40, 168

Ta có: (24=2^{3}.3); (40=2^{3}.5); (168=2^{3}.3.7)

Vậy (BCNN(24,40,168)=2^{3}.3.5.7=840).

Bội số chung nhỏ nhất được hiểu là số nhỏ nhất khác 0 có thể chia hết cho 2 hoặc nhiều số tự nhiên khác

Số nguyên tố là gì?

Một số tự nhiên (1, 2, 3, 4, 5, 6, …) được gọi là số nguyên tố nếu nó lớn hơn 1 và không thể được biểu diễn thành tích của hai số tự nhiên nhỏ hơn. Các số lớn hơn 1 không phải là số nguyên tố được gọi là hợp số. Nói cách khác,n là số nguyên tố nếu n vật không thể chia đều thành nhiều nhóm nhỏ gồm nhiều hơn một vật, hoặc n dấu chấm không thể được sắp xếp thành một hình chữ nhật có chiều dài và chiều rộng nhiều hơn một dấu chấm. Chẳng hạn, trong các số từ 1 đến 6, số 2, 3 và 5 là số nguyên tố vì không có số nào khác có thể chia hết được chúng (số dư bằng 0). 1 không phải là số nguyên tố vì nó đã được loại trừ ra khỏi định nghĩa. 4 = 2 × 2 và 6 = 2 × 3 đều là hợp số.

 

Hình minh họa cho thấy 7 là số nguyên tố vì không có số nào trong các số 2, 3, 4, 5, 6 có thể chia hết 7

Ước số của một số tự nhiên n là các số tự nhiên có thể chia hết được n. Mọi số tự nhiên đều có ít nhất hai ước số là 1 và chính nó. Nếu nó còn có thêm một ước số khác thì nó không thể là số nguyên tố. Từ ý tưởng đó mà ta có một định nghĩa khác về số nguyên tố: đó là những số chỉ có đúng hai ước số dương là 1 và chính nó. Ngoài ra, còn có một cách diễn đạt khác nữa: n là số nguyên tố nếu nó lớn hơn 1 và không có số nào trong các số 2, 3,….n-1 có thể chia hết được nó.

25 số nguyên tố đầu tiên (tất cả các số nguyên tố nhỏ hơn 100) là:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 (dãy số A000040 trong bảng OEIS).

Không có số chẵn nào lớn hơn 2 nào là số nguyên tố. Do đó, tất cả số nguyên tố ngoài số 2 là số lẻ và được gọi là số nguyên tố lẻ. Tương tự, khi được viết trong hệ thập phân, tất cả số nguyên tố lớn hơn 5 đều có tận cùng là 1, 3, 7 hoặc 9. Các số có tận cùng là chữ số khác đều là hợp số: số có tận cùng là 0, 2, 4, 6 hoặc 8 là số chẵn, và số có tận cùng là 0 hoặc 5 thì chia hết cho 5.

Hợp số là gì?

Hợp là là các số tự nhiên lớn hơn 1 và phải chia hết cho một số tư nhiên khác 1 và chính nó. Hay nói cách khác hợp số là số tự nhiên lớn hơn một, chia hết cho 1, chia hết cho chính nó, và phải chia hết cho một số tự nhiên khác. Ví dụ hợp số trong khoảng từ 1 đến 100 là <4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100>.

Ứng dụng của ước chung và bội chung

Ứng dụng liên quan đến chia hết

Dựa vào định nghĩa và một số tính chất của quan hệ chia hết. Định nghĩa: cho 2 số nguyên a và b với b khác 0. Nếu có một số nguyên q sao cho a = bq thì ta nói rằng b chia hết cho a hay b là ước của a.

Tính chất chia hết của 2 số: a ⋮ b khi a = b.q.

Bài tập áp dụng: thường là các bài toán chứng minh chia hết.

Ứng dụng vào giải phương trình nghiệm nguyên

Phương trình có thể tách thành nhân tử.

Bài toán áp dụng : giải phương trình nghiệm nguyên có thể tách thành nhân tử, ứng dụng cách tìm ước của 1 số.

Xem thêm: Người Sinh Ngày 15 Tháng 6 Cung Gì ? Người Sinh 15 Tháng 6 Là Cung Hoàng Đạo Gì

Ứng dụng vào xét một số bài toán liên quan đến chia hết

Dựa vào định nghĩa và tính chất của quan hệ chia hết,của ƯC,ƯCLN và BC,BCNN

Bài toán áp dụng :thường là những bài toán liên quan đến thực tế. Có thể ứng dụng ước chung lớn nhất hoặc bội chung nhỏ nhất tùy bài áp dụng.

Cách tìm ước chung lớn nhất

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là UCLN cần tìm.

Chú ý:

Hai số nguyên tố cùng nhau khi và chỉ khi ước chung lớn nhất của hai số bằng 1.

Cách tìm Ước chung thông qua tìm UCLN.

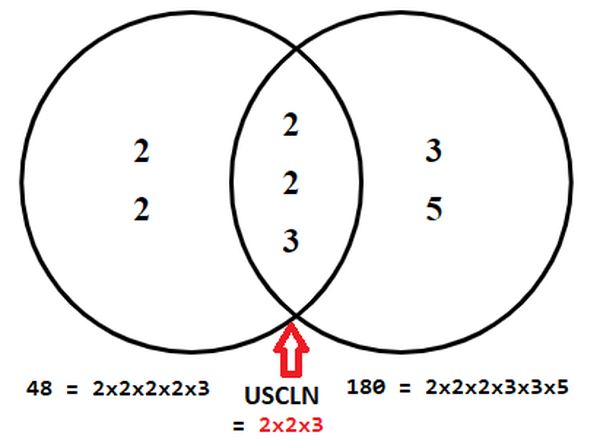
Cách tìm bội số chung nhỏ nhất

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN cần tìm.

Chú ý:

Nếu hai số a, b là hai số nguyên tố cùng nhau thì BCNN là tích của a.b

Nếu a là bội của b thì a cũng chính là BCNN của hai số a, b.

Bài tập vận dụng Ước và Bội của số nguyên

Trong chương trình số học lớp 6, sau khi học các khái niệm ước chung lớn nhất (ƯCLN) và bội chung nhỏ nhất (BCNN), các bạn sẽ gặp dạng toán tìm hai số nguyên dương khi biết một số yếu tố trong đó có các dữ kiện về ƯCLN và BCNN.

Phương pháp chung để giải:

1/ Dựa vào định nghĩa ƯCLN để biểu diễn hai số phải tìm, liên hệ với các yếu tố đã cho để tìm hai số.

2/ Trong một số trường hợp, có thể sử dụng mối quan hệ đặc biệt giữa ƯCLN, BCNN và tích của hai số nguyên dương a, b, đó là: ab = (a, b)., trong đó (a, b) là ƯCLN và là BCNN của a và b. Việc chứng minh hệ thức này không khó

Theo định nghĩa ƯCLN, gọi d = (a, b) => a = md; b = nd với m, n thuộc Z+; (m, n) = 1 (*)

Từ (*) => ab = mnd2;

= mnd

=> (a, b).

= d.(mnd) = mnd2 = ab

=> ab = (a, b).

. (**)

Hãy xét một số ví dụ minh họa.

Bài toán 1: Tìm hai số nguyên dương a, b biết

= 240 và (a, b) = 16.

Lời giải: Do vai trò của a, b là như nhau, không mất tính tổng quát, giả sử a ≤ b.

Từ (*), do (a, b) = 16 nên a = 16m; b = 16n (m ≤ n do a ≤ b) với m, n thuộc Z+; (m, n) = 1.

Theo định nghĩa BCNN:

= mnd = mn.16 = 240 => mn = 15

=> m = 1, n = 15 hoặc m = 3, n = 5 => a = 16, b = 240 hoặc a = 48, b = 80.

Chú ý: Ta có thể áp dụng công thức (**) để giải bài toán này: ab = (a, b).

=> mn.162 = 240.16 suy ra mn = 15.

Bài toán 2: Tìm hai số nguyên dương a, b biết ab = 216 và (a, b) = 6.

Lời giải: Lập luận như bài 1, giả sử a ≤ b.

Do (a, b) = 6 => a = 6m; b = 6n với m, n thuộc Z+; (m, n) = 1; m ≤ n.

Xem thêm:

Cơm Chó Là Gì – Ý Nghĩa Thú Vị Của Cụm Từ Ăn Cơm Chó

Vì vậy: ab = 6m.6n = 36mn => ab = 216 tương đương mn = 6 tương đương m = 1, n = 6 hoặc m = 2, n = 3 tương đương với a = 6, b = 36 hoặc là a = 12, b = 18.