Bài 19 Cho Hình Chóp Sabc – Cho Hình Chóp Sabc Có Sa Vuông Góc ( (Abc) )

Cho hình chóp $SABC$ có $SA ot left( {ABC}
ight).$ Gọi $H,{
m{ }}K$ lần lượt là trực tâm các tam giác $SBC$ và$ABC$. Mệnh đề nào sai trong các mệnh đề sau?

Phương pháp giải

Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để xét tính đúng, sai của các đáp án.

Đang xem: Cho hình chóp sabc

Lời giải của GV sonlavn.com

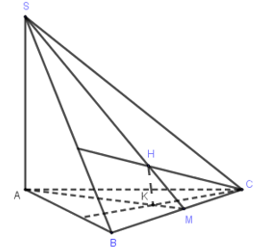
Ta có(BC ot SA,,BC, ot SH,, Rightarrow ,BC ot (SAH))

Ta có (CK ot AB,CK ot SA Rightarrow CK ot (SAB)) hay (CK ot SB)

Mặt khác có (CH ot SB) nên (SB ot (CHK)) hay (SB ot HK).

Ta có:

(left{ egin{array}{l}BK ot AC\BK ot SAend{array}
ight. ) (Rightarrow BK ot left( {SAC}
ight) Rightarrow BK ot SC)

Mà (BH ot SC) nên (SC ot (BHK)) nên (SC ot HK).

Do đó (HK ot (SBC)).

Gọi (M) là giao điểm của (SH) và (BC). Do (BC ot (SAH),, Rightarrow BC ot AM) hay đường thẳng

(AM) trùng với đường thẳng (AK). Hay $SH,AK$ và $BC$ đồng quy.

Do đó $BC ot left( {SAB}
ight)$ là sai.

Đáp án cần chọn là: c

…

Xem thêm: Confession Là Gì – Và Trào Lưu Confession

Câu hỏi liên quan

Cho hình chóp (S.ABCD) có (SA ot left( {ABCD}
ight)) và (AB ot BC). Dựng (AH) là đường cao của (Delta SAB). Khẳng định nào sau đây sai?

Cho tứ diện $SABC$ có $ABC$ là tam giác vuông tại $B$ và $SA ot left( {ABC}
ight)$. Gọi $AH$ là đường cao của tam giác $SAB$, thì khẳng định nào sau đây đúng nhất.

Cho tứ diện $ABCD$có (AB = AC) và (DB = DC). Khẳng định nào sau đây đúng?

Cho hình chóp (S.ABC) có (SA ot (ABC)) và (AB ot BC.) Số các mặt của tứ diện (S.ABC) là tam giác vuông là:

Cho hình chóp (S.ABC) có đáy (ABC) là tam giác đều cạnh (a) và độ dài các cạnh bên (SA = SB = SC = b.) Gọi (G) là trọng tâm của tam giác (ABC.) Độ dài đoạn thẳng (SG) bằng

Cho hình chóp (S.ABCD) có đáy (ABCD) là hình chữ nhật, (SA ot left( {ABCD}
ight)). Gọi (AE;AF) lần lượt là các đường cao của tam giác (SAB) và tam giác $SAD$. Gọi (M) là giao điểm của (SC) với ( (AEF) ). Chọn khẳng định đúng trong các khẳng định sau ?

Cho hình chóp (S.ABC) có cạnh (SA ot left( {ABC}
ight)) và đáy (ABC) là tam giác cân ở (C). Gọi (H) và (K) lần lượt là trung điểm của (AB) và (SB). Khẳng định nào sau đây sai?

Cho tứ diện (OABC) có (OA,OB,OC) đôi một vuông góc với nhau. Gọi (H) là hình chiếu của (O) trên (mp(ABC)). Mệnh đề nào sai trong các mệnh đề sau:

Cho tứ diện (ABCD) có (AB ot CD) và (AC ot BD). Gọi (H) là hình chiếu vuông góc của (A) lên (mp(BCD)). Các khẳng định sau, khẳng định nào sai?

Cho hình chóp $SABC$ có $SA ot left( {ABC}
ight).$ Gọi $H,{
m{ }}K$ lần lượt là trực tâm các tam giác $SBC$ và$ABC$. Mệnh đề nào sai trong các mệnh đề sau?

Cho hai hình chữ nhật $ABCD$ và $ABEF$ nằm trong hai mặt phẳng khác nhau sao cho hai đường thẳng $AC$ và $BF$ vuông góc với nhau. Gọi $CH$ và $FK$ lần lượt là đường cao của hai tam giác $BCE$ và $ADF$.

Khẳng định nào sau đây là sai?

Cho hình chóp (S.ABCD) có đáy (ABCD) là hình vuông và (SA ot left( {ABCD}
ight)). Gọi (I), (J), (K) lần lượt là trung điểm của (AB), (BC) và (SB). Khẳng định nào sau đây sai?

Cho hình tứ diện (ABCD) có $AB$, $BC$, $CD$ đôi một vuông góc nhau. Hãy chỉ ra điểm (O) cách đều bốn điểm (A), (B), (C), (D).

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, mặt bên $SAB$ là tam giác đều và $SC = asqrt 2 $. Gọi $H,K$ lần lượt là trung điểm của các cạnh $AB$ và $AD$.Khẳng định nào sau đây là sai?.

Cho hình chóp $S.ABC$ có $widehat {BSC} = {120^0},widehat {CSA} = {60^0},widehat {ASB} = {90^0},$ $SA = SB = SC.$ Gọi $I$ là hình chiếu vuông góc của $S$ lên $mpleft( {ABC}
ight).$ Chọn khẳng định đúng trong các khẳng định sau

Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau. Gọi $H$ là hình chiếu của $O$ trên mặt phẳng $left( {ABC}
ight)$. Xét các mệnh đề sau :

I. Vì $OC ot OA,OC ot OB$ nên $OC ot left( {OAB}
ight)$.

Xem thêm: Jung So Min, Tin Tức Mới Nhất Vụ Tân Binh Bị “Hất Cẳng” Khỏi Phim Vì Diễn Kém Lên Top 1 Hot Search Trung, Ekip Thanh Minh Nhưng Netizen Chả Tin

II. Do $AB subset left( {OAB}
ight)$nên $AB ot OC.{
m{ }}left( 1
ight)$

III. Có $OH ot left( {ABC}
ight)$ và $AB subset left( {ABC}
ight)$nên $AB ot OH.{
m{ }}left( 2
ight)$

IV. Từ $left( 1
ight)$ và $left( 2
ight) Rightarrow AB ot left( {OCH}
ight)$

Số mệnh đề đúng trong các mệnh đề trên là:

Cho hình hộp $ABCD.A”B”C”D”$ có đáy là hình thoi $widehat {BAD} = {60^0}$ và $A”A = A”B = A”D$. Gọi $O = AC cap BD$. Hình chiếu của $A”$ trên $left( {ABCD}
ight)$ là :

Cơ quan chủ quản: Công ty Cổ phần công nghệ giáo dục Thành Phát

Tel: 0247.300.0559

gmail.com

Trụ sở: Tầng 7 – Tòa nhà Intracom – Trần Thái Tông – Q.Cầu Giấy – Hà Nội

Giấy phép cung cấp dịch vụ mạng xã hội trực tuyến số 240/GP – BTTTT do Bộ Thông tin và Truyền thông.