Tổng Hợp Các Công Thức Tích Phân Là Gì? Bảng Công Thức Tính Tích Phân Thường Gặp

Một chủ đề quan trọng thường xuất hiện trong đề thi là tích phân, muốn học tốt phần này bạn cần nhớ bảng công thức tích phân cơ bản, biết cách vận dụng những công thức này sao cho hiệu quả. Bài viết này sẽ giúp bạn.

Một chủ đề quan trọng thường xuất hiện trong đề thi là tích phân, muốn học tốt phần này bạn cần nhớ bảng công thức tích phân cơ bản, biết cách vận dụng những công thức này sao cho hiệu quả. Bài viết này sẽ giúp bạn.

Đang xem: Công thức tích phân

Để học hiệu quả bài này, bạn nên học theo trình tự từ lý thuyết, các công thức tích phân cơ bản, các dạng bài tích phân thường gặp. Sau khi học kĩ lý thuyết bạn nên các bài tập minh họa ở phần cuối.

1. Tích phân là gì?

Tích phân là kiến thức quan trọng trong giải tích lớp 12. Ứng dụng quan trọng của tích phân dùng để tính diện tích và thể tích của vật thể..

2. Bảng công thức tích phân cơ bản

Ngoài khái niệm, muốn giải tốt tích phân bạn cần nhớ chính xác những công thức tích phân cơ bản dưới đây:

3. Phương pháp giải tích phân

3.1 Tính tích phân sử dụng bảng nguyên hàm cơ bản

3.2 Tích phân có chứa dấu giá trị tuyệt đối

3.3 Phương pháp đổi biến số trong tích phân

Một trong những phương pháp thường dùng trong giải bài toán tích phân là đổi biến số, nghĩa là thông qua các đổi biến ta đưa một tích phân từ phức tạp về tích phân cơ bản. Từ đây ta dựa vào bảng tích phân để suy ra kết quả.

3.4 Cách tính tích phân từng phần

Một phương pháp khá hay được nhiều thầy cô dạy đó là phương pháp tính tích phân từng phần, đây là phương pháp quan trọng giải được nhiều bài tập khó trong đề thi THPT Quốc gia. Phương pháp này có 1 công thức tổng quát và 4 dạng toán thường gặp.

Công thức tích phân từng phần tổng quát:

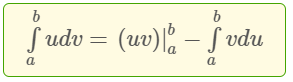
Lưu ý: Chúng ta thường hay gặp 4 dạng tích phân từng phần

Dạng 1: Tích phân hàm số mũ

Dạng 2: Tích phân hàm số logarit

Dạng 3: Tích phân lượng giác

Dạng 4: Tích phân hàm phức hợp giữa đa thức và lượng giác

4. Bài tập

Bài tập 1. (Câu 18 trích đề thi minh họa lần 2 năm 2019 – 2020)

Bài tập 2. (Vận dụng phương pháp đổi biến số giải câu 33 trích đề thi minh họa lần 2 năm 2019 – 2020)

Bài tập 3. (Giải câu 45 trích đề thi minh họa lần 2 năm 2019 – 2020)

Bài tập 4. Cho số thực a thỏa mãn $intlimits_{ – 1}^a {{e^{x + 1}}dx} = {e^2} – 1$, khi đó a có giá trị bằng

A. 1.

B. – 1.

C. 0.

D. 2.

Hướng dẫn giải

Ta có $intlimits_{ – 1}^a {{e^{x + 1}}dx} = left. {{e^{x + 1}}}
ight|_{ – 1}^a = {e^{a + 1}} – e$.

Vậy yêu cầu bài toán tương đương ${e^{a + 1}} – 1 = {e^2} – 1{ ext{ }} Leftrightarrow { ext{ }}a = 1$.

Bài tập 5. Nếu $intlimits_{ – 2}^0 {left( {4 – {e^{ – x/2}}}
ight)dx} = K – 2e$ thì giá trị của K là

A. 12,5.

Xem thêm: Phân Biệt Câu Hỏi Tu Từ Là Gì ? Biện Pháp Tu Từ Là Gì

B. 9.

C. 11.

D. 10.

Hướng dẫn giải

$egin{array}{*{20}{l}} egin{array}{l} K = intlimits_{ – 2}^0 {left( {4 – {e^{ – x/2}}}
ight)dx} + 2e\ = left. {left( {4x + 2{e^{ – x/2}}}
ight)}
ight|_{ – 2}^0 + 2e end{array}\ { = 2 – left( { – 8 + 2e}
ight) + 2e = 10} end{array}$

Bài tập 6. Tích phân $I = intlimits_{ – 2}^0 {x{e^{ – x}}dx} $ có giá trị bằng

A. $ – {e^2} + 1$.

B. $3{e^2} – 1$.

C. $ – {e^2} – 1$.

D. $ – 2{e^2} + 1$.

Hướng dẫn giải

Sử dụng tích phân từng phần, ta được

$egin{array}{l} I = intlimits_{ – 2}^0 {x{e^{ – x}}dx} \ = – intlimits_{ – 2}^0 {xdleft( {{e^{ – x}}}
ight)} \ = – left< {left. {left( {x{e^{ – x}}} ight)} ight|_{ – 2}^0 – intlimits_{ – 2}^0 {{e^{ – x}}dx} } ight>\ = – left. {left( {x{e^{ – x}}}
ight)}
ight|_{ – 2}^0 + intlimits_{ – 2}^0 {{e^{ – x}}dx} \ = – left. {left( {x{e^{ – x}}}
ight)}
ight|_{ – 2}^0 – left. {left( {{e^{ – x}}}
ight)}
ight|_{ – 2}^0\ = – {e^2} – 1. end{array}$

Bài tập 7. Cho hàm số f liên tục trên đoạn < 0;, 3>. Nếu $intlimits_0^3 {f(x)dx} = 2$ thì tích phân $intlimits_0^3 {left< {x – 2f(x)} ight>dx} $ có giá trị bằng

A. 7.

B. 2,5.

C. 5.

D. 0,5.

Xem thêm: Tin Học 10 Bài 8 Tin Học 10 Bài 8: Những Ứng Dụng Của Tin Học

Hướng dẫn giải

$egin{array}{l} intlimits_0^3 {left< {x – 2f(x)} ight>dx} \ = intlimits_0^3 {xdx} – 2intlimits_0^3 {f(x)dx} \ = frac{9}{2} – 2 imes 2 = frac{1}{2} end{array}$

Hy vọng với bài viết về công thức tích phân, phương pháp đổi biến số, cách tính tích phân từng phần ở trên hữu ích với bạn. Thấy hay hãy chia sẻ tới mọi người và nhớ quay lại sonlavn.com để xem những chủ đề tiếp theo nhé.