Dấu Của Nhị Thức Bậc Nhất, Bất Phương Trình Bậc Nhất, Giải Toán 10 Bài 3

Đối với nhiều bạn học sinh, việc giải các bài tập vận dụng dấu của nhị thức bậc nhất hay bất phương trình bậc nhất không gặp nhiều khó khăn, bởi phần nội dung kiến thức này cũng không quá khó.

Đang xem: Dấu của nhị thức bậc nhất

Tuy nhiên, để các em dễ dàng ghi nhớ và giải các bài tập về bất phương trình bậc nhất, hay các bài tập vận dụng dấu của nhị thức bậc nhất một cách nhuần nhuyễn, chúng ta cùng hệ thống lại một số dạng bài tập về nội dung này, đặc biệt là dạng bài tập biện luận, có dấu trị tuyệt đối và căn thức.

I. Kiến thức cần nhớ

1. Bất phương trình ẩn x

– Bất phương trình ẩn x là những bất phương trình có dạng:

 f(x) g(x); (2)

2. Bất phương trình bậc nhất một ẩn

– Bất phương trình bậc nhất một ẩn có dạng:

 ax + b 0 (4)

 ax + b ≤ 0 (5)

 ax + b ≥ 0 (6)

– Tập nghiệm: Xét ax + b 0: 

 Nếu a 3. Dấu của nhị thức bậc nhất f(x) = ax + b

– Ta có bảng xét dấu như sau:

4. Hệ bất phương trình bậc nhất

¤ Gọi S1 và S2 là tập nghiệm của bất phương trình (1): ax + b 0.

◊ (1) và (2) có nghiệm ⇔ S1 ∩ S2 ≠ Ø

◊ (1) và (2) vô nghiệm ⇔ S1 ∩ S2 = Ø

◊ (1) tương đương (2) ⇔ S1 = S2

◊ (2) là hệ quả của (1) ⇔ S2 ⊂ S1

II. Bài tập vận dụng dấu của nhị thức bậc nhất, bất phương trình bậc nhất

° Dạng 1: Giải và biện luận bất phương trình bậc nhất

* Phương pháp:

– Có: ax + b 0: 

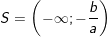
 ♦ Nếu a 2(x – 2) > x – 2m. (*)

° Lời giải:

– Ta có: (*) ⇔ m2x – 2m2 > x – 2m

 ⇔ m2x – x > 2m2 – 2m

 ⇔ (m2 – 1)x > 2m(m – 1) (**)

– Trường hợp 1: Nếu m2 – 1 = 0 ⇔ m = 1 hoặc m = -1

Nếu m = 1 thay vào (**) ta được: 0x > 0 (vô nghiệm)

Nếu m = -1 thay vào (**) ta được: 0x > 4 (vô nghiệm)

– Trường hợp 2: Nếu m2 – 1 > 0 ⇔ m > 1 hoặc m frac{2m}{m+1}” src=”https://sonlavn.com/uploads/news/wyswyg/2019_11/1573751088t41q4pewwn.gif” />

– Trường hợp 3: Nếu m2 – 1 1 thì 

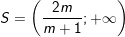
* Ví dụ 2: Giải và biện luận bất phương trình: 

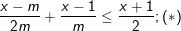
° Lời giải:

– Ta có: 

 (**)

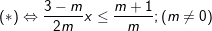
– Lập bảng xét dấu của nhị thức bậc nhất này như sau:

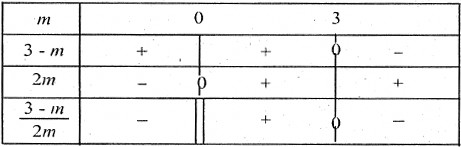
– Từ bảng xét dấu nhị thức bậc nhất ở trên ta có:

 ♦ m = 3 từ (**) ta có: 

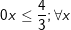
 ♦ m 3 từ (**) ta có: 

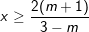
 ♦ 0 3 thì

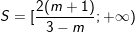
° Dạng 2: Xét dấu các nhị thức bậc nhất để giải biện luận bất phương trình bậc nhất

* Phương pháp:

– Vận dụng tính chất dấu của nhị thức bậc nhất

* Ví dụ 1: Giải và biện luận bất phương trình (x+m)(x-m+2)≥0 (*)

° Lời giải:

– Xét hàm: f(x) = (x+m)(x-m+2)

– Nếu f(x) = 0 ⇒ x = -m hoặc x = m – 2

♠ Trường hợp 1: m – 2 > -m ⇒ m > 1 ta có bảng xét dấu:

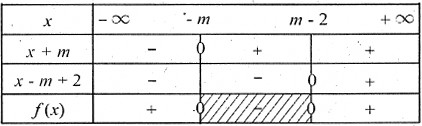
– Từ bảng xét dấu trên ta có tập nghiệm: S = (-∞;-m> ∪

♠ Trường hợp 2: m – 2 = -m ⇒ m = 1 ta có: S = R

♠ Trường hợp 3: m – 2 2 thì từ (*) ta có: 

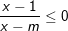
– Ta có bảng xét dấu như sau:

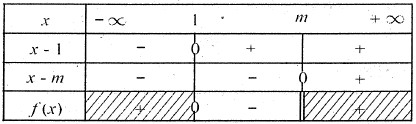
– Từ bảng xét dấu ta có tập nghiệm: 1 ≤ x ° Dạng 3: Bất phương trình có chứa dấu giá trị tuyệt đối

* Phương pháp: – Vận dụng các tính chất:

♦ 

♦ 

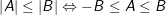
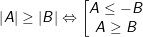
* Ví dụ 1: Giải bất phương trình: |1 – x| + |x – 2| > |x – 4| (*)

° Lời giải:

– Ta lập bảng xét dấu như sau:

♦ Từ bảng xét dấu ta có:

– TH1: x 3 (không thỏa).

– TH3: 2 7/3 suy ra (7/3) -1 suy ra x ≥ 4.

Xem thêm: Bài Soạn Văn 8 Miêu Tả Và Biểu Cảm Trong Văn Bản Tự Sự Trang 72

♦ Kết luận, tập nghiệm của (*) là: 

* Ví dụ 2: Giải bất phương trình: |mx – 1| 3 – 2m. (**)

– TH1: m = 0: từ (**) ta được: 

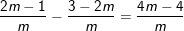
 ta có bảng sau:

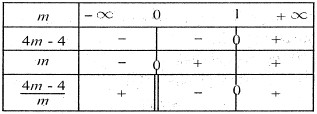
 0 1 (vô nghiệm).

 m>1 thì ta có 

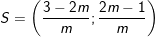
III. Một số Bài tập về bất phương trình, dấu của nhị thức bậc nhất.

* Bài tập 1: Giải các bất phương trình

a) |x| – |x – 2| ≤ 2|x – 4|

b) 

* Bài tập 2: Giải và biện luận bất phương trình: 

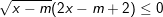
* Bài tập 3: Giải và biện luận bất phương trình: 

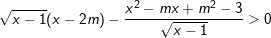
Đối với bài tập về xét dấu nhị thức còn có thêm dạng bài tập xét dấu của tích hoặc thương nhiều nhị thức bậc nhất (gần giống dạng 2 và 3 ở trên) tuy nhiên nội dung này chúng ta sẽ đề cập chi tiết hơn ở phần bài tập xét dấu tam thức bậc 2.

Xem thêm: Bankplus Mb Là Gì? Cách Chuyển Tiền Qua Bankplus Mb Online Nhanh Nhất

Với việc vận dụng việc xét dấu của nhị thức bậc nhất để giải các bài tập về bất phương trình bậc nhất ở trên cho thấy sự chặt chẽ trong cách giải, qua đó việc giải các bài toán thuộc loại tương đối khó là biện luận cũng được rõ ràng và dễ hiểu hơn.