Cách Chứng Minh Hai Mặt Phẳng Vuông Góc Trong Không Gian Cực Hay

Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng vuông góc với nhau.

Đang xem: Hai mặt phẳng vuông góc

c) Tính chất

– Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến đều vuông góc với mặt phẳng kia.

– Nếu hai mặt phẳng (left( P
ight),left( Q
ight)) vuông góc với nhau và (A in left( P
ight)) thì đường thẳng (a) qua (A) và vuông góc với (left( Q
ight)) sẽ nằm trong (left( P
ight)).

– Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ ba.

– Qua đường thẳng (a) không vuông góc với mặt phẳng (left( Q
ight)), có duy nhất một mặt phẳng (left( P
ight)) vuông góc với (left( Q
ight)).

2. Bài toán về quan hệ vuông góc

a) Chứng minh hai mặt phẳng vuông góc

Phương pháp chung:

Tìm một đường thẳng (a) nằm trong mặt phẳng (left( P
ight)) mà (a ot left( Q
ight)).

Ví dụ: Cho tứ diện (ABCD) có (AB ot left( {BCD}
ight)). Gọi (E) là hình chiếu của (B) trên (CD). Chứng minh (left( {ABE}
ight) ot left( {ACD}
ight)).

Xem thêm: Công Nghiệp Hóa Là Gì ? Khái Niệm, Vai Trò Công Nghiệp Hóa

Giải:

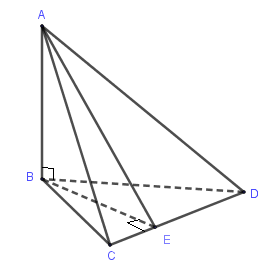
Để chứng minh (left( {ACD}
ight) ot left( {ABE}
ight)) ta sẽ tìm một đường thẳng trong mặt phẳng này mà nó vuông góc với mặt phẳng kia.

Thật vậy,

Ta có: (AB ot left( {BCD}
ight) Rightarrow AB ot CD).

Lại có (BE ot CD) nên (CD ot left( {ABE}
ight)).

Mà (CD subset left( {ACD}
ight)) nên (CD) chính là đường thẳng nằm trong mặt phẳng (left( {ACD}
ight)) mà vuông góc với (left( {ABE}
ight)).

Vậy (left( {ACD}
ight) ot left( {ABE}
ight)).

b) Chứng minh đường thẳng vuông góc mặt phẳng

Phương pháp chung:

Ngoài một số phương pháp đề cập từ bài trước, ta có thể sử dụng thêm một trong các phương pháp dưới đây:

+) Chứng minh (a subset left( Q
ight)) với (left( Q
ight) ot left( P
ight)) và (a) vuông góc với giao tuyến của (left( P
ight)) và (left( Q
ight)).

Xem thêm: Tóm Tắt Văn Bản Chiếc Lá Cuối Cùng Của O, Tóm Tắt Truyện Ngắn Chiếc Lá Cuối Cùng Của O

+) Chứng minh (a) là giao tuyến của hai mặt phẳng (left( Q
ight),left( R
ight)) mà cùng vuông góc với (left( P
ight)).