Đường Trung Bình Của Hình Thang, Đường Trung Bình Của Tam Giác, Của Hình Thang

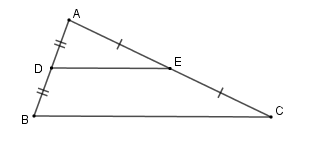
+ (Delta ABC) có (D) là trung điểm của (AB) , (E) là trung điểm của (AC) nên (DE) là đường trung bình của tam giác (ABC) ( Rightarrow DE{
m{//}}BC;,DE = dfrac{1}{2}BC.)

+ Nếu (left{ egin{array}{l}DA = DB\DE{
m{//}}BCend{array}
ight. Rightarrow EC = EA) .

Đang xem: đường trung bình của hình thang

Đường trung bình của hình thang

Ví dụ:

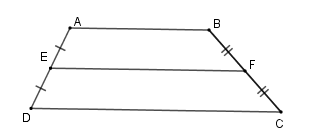
+ Hình thang (ABCD) (hình vẽ) có (E) là trung điểm (AD) , (F) là trung điểm của (BC) nên (EF) là đường trung bình của hình thang ( Rightarrow left{ egin{array}{l}EF{
m{//}}DC\EF = dfrac{{AB + DC}}{2}end{array}
ight.)

2. Các dạng toán thường gặp

Dạng 1: Chứng minh các hệ thức về cạnh và góc. Tính các cạnh và góc.

Phương pháp:

Sử dụng tính chất đường trung bình của tam giác và hình thang.

+ Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

+ Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Xem thêm: Tổng Giám Đốc Tiếng Anh Là Gì, Chức Danh Trong Công Ty Bằng Tiếng Anh

+ Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

Dạng 2: Chứng minh một cạnh là đường trung bình của tam giác, hình thang.

Phương pháp:

Sử dụng định nghĩa đường trung bình của tam giác và hình thang.

+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

Xem thêm: Văn Bản Từ Chối Tài Sản Chung Của Vợ Chồng, Please Wait

+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

Mục lục – Toán 8
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
Bài 1: Phép nhân đơn thức với đa thức, đa thức với đa thức
Bài 2: Những hằng đẳng thức đáng nhớ
Bài 3: Các hằng đẳng thức đáng nhớ (tiếp)
Bài 4: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Bài 5: Phân tích đa thức thành nhân tử bằng cách dùng hằng đẳng thức
Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
Bài 7: Phối hợp nhiều phương pháp phân tích đa thức thành nhân tử
Bài 8: Chia đơn thức cho đơn thức
Bài 9: Chia đa thức một biến đã sắp xếp
Bài 10: Ôn tập chương 1
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
Bài 1: Phân thức đại số
Bài 2: Rút gọn phân thức đại số
Bài 3: Qui đồng mẫu thức nhiều phân thức
Bài 4: Cộng, trừ các phân thức
Bài 5: Nhân, chia các phân thức hữu tỉ
Bài 6: Biến đổi các phân thức hữu tỉ
Bài 7: Ôn tập chương 2: Phân thức đại số
CHƯƠNG 3: PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1: Mở đầu về phương trình
Bài 2: Phương trình bậc nhất một ẩn và cách giải
Bài 3: Phương trình tích
Bài 4: Phương trình chứa ẩn ở mẫu
Bài 5: Giải bài toán bằng cách lập phương trình
Bài 6: Ôn tập chương 3: Phương trình bậc nhất một ẩn
CHƯƠNG 4: BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1: Liên hệ giữa thứ tự và phép cộng
Bài 2: Liên hệ giữa thứ tự và phép nhân
Bài 3: Bất phương trình bậc nhất một ẩn
Bài 4: Phương trình chứa dấu giá trị tuyệt đối
Bài 5: Ôn tập chương 4: Bất phương trình bậc nhất một ẩn
CHƯƠNG 5: TỨ GIÁC
Bài 1: Tứ giác
Bài 2: Hình thang
Bài 3: Đường trung bình của tam giác, hình thang
Bài 4: Đối xứng trục
Bài 5: Hình bình hành
Bài 6: Đối xứng tâm
Bài 7: Hình chữ nhật
Bài 8: Hình thoi
Bài 9: Hình vuông
Bài 10: Ôn tập chương 5: Tứ giác
CHƯƠNG 6: ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
Bài 1: Đa giác, đa giác đều
Bài 2: Diện tích hình chữ nhật, diện tích tam giác
Bài 3: Diện tích hình thang, diện tích hình thoi
Bài 4: Ôn tập chương 6: Đa giác, diện tích đa giác
CHƯƠNG 7: TAM GIÁC ĐỒNG DẠNG
Bài 1: Định lí Ta-lét. Định lí đảo và hệ quả của định lí Ta-lét
Bài 2: Tính chất đường phân giác của tam giác
Bài 3: Hai tam giác đồng dạng
Bài 4: Trường hợp đồng dạng thứ nhất
Bài 5: Trường hợp đồng dạng thứ hai
Bài 6: Trường hợp đồng dạng thứ ba
Bài 7: Các trường hợp đồng dạng của tam giác vuông
Bài 8: Ôn tập chương 7: TAM GIÁC ĐỒNG DẠNG
CHƯƠNG 8: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
Bài 1: Hình hộp chữ nhật
Bài 2: Thể tích hình hộp chữ nhật
Bài 3: Hình lăng trụ đứng
Bài 4: Hình chóp đều, hình chóp cụt đều
Bài 5: Ôn tập chương 8: Hình lăng trụ đứng. Hình chóp đều

Học toán trực tuyến, tìm kiếm tài liệu toán và chia sẻ kiến thức toán học.

sonlavn.com
Theo dõi chúng tôi trên