Trigonometry Calculator – Summary Of Trigonometric Identities

Take an x-axis and an y-axis (orthonormal) and let O be the origin. A circle centered in O and with radius = 1is known as trigonometric circle or unit circle.

Đang xem: Trigonometry calculator

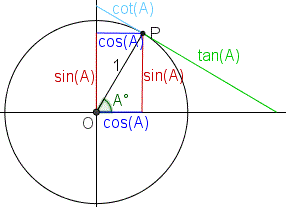
If P is a point from the circle and A is the angle between PO and x axis then:the x-coordinate of P is called the cosine of A. We write cos(A) or cos A;the y-coordinate of P is called the sine of A. We write sin(A) or sin A;the number sin(A)/cos(A) is called the tangent of A. We write tan(A) or tan A;the number cos(A)/sin(A) is called the cotangent of A. We write cot(A) or cot A.
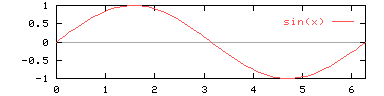
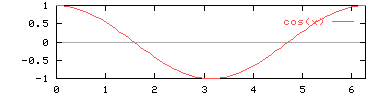
The sine function

sin : R -> RAll trigonometric functions are periodic. The period of sin is 2$pi$.The range of the function is <-1,1>.

Xem thêm: Giải Ngố Pga Là Gì ? Phân Loại Pga? Chi Phí Pga Có Cao Không?

The tangent function

tan : R -> RThe range of the function is R.Now, the period is $pi$ and the function is undefined at x = ($pi$/2) + k$pi$, k=0,1,2,…The graph of the tangent function on the interval 0 – $pi$

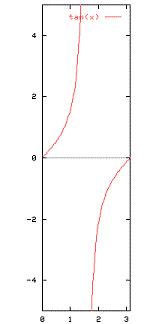
Animated graph(open in a new window):The graph of the tangent function on the interval 0 – 2$pi$

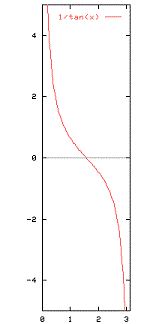
The cotangent function

cot : R -> RThe range of the function is R.The period is $pi$ and that the function is undefined at x = k$pi$, k=0,1,2,…

Xem thêm: Làm Thơ Lục Bát – Cách Đơn Giản, Thú Vị Để Tặng Bạn Bè, Người Thân

The values of sin, cos, tan, cot at the angles of 0°, 30°, 60°, 90°, 120°,135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°

$A^o$$0^o$$30^o$$45^o$$60^o$$90^o$$120^o$$135^o$$150^o$$180^o$$210^o$$225^o$$240^o$$270^o$$300^o$$315^o$$330^o$$360^o$

$A rad$

$0$

$frac{pi}{6}$

$frac{pi}{4}$

$frac{pi}{3}$

$frac{pi}{2}$

$frac{2pi}{3}$

$frac{3pi}{4}$

$frac{5pi}{6}$

$pi$

$frac{7pi}{6}$

$frac{5pi}{4}$

$frac{4pi}{3}$

$frac{3pi}{2}$

$frac{5pi}{3}$

$frac{7pi}{4}$

$frac{11pi}{6}$

$2pi$

$sin A$

$0$

$frac{1}{2}$

$frac{sqrt{2}}{2}$

$frac{sqrt{3}}{2}$

$1$

$frac{sqrt{3}}{2}$

$frac{sqrt{2}}{2}$

$frac{1}{2}$

$0$

$-frac{1}{2}$

$-frac{sqrt{2}}{2}$

$-frac{sqrt{3}}{2}$

$-1$

$-frac{sqrt{3}}{2}$

$-frac{sqrt{2}}{2}$

$-frac{1}{2}$

$0$

$cos A$

$1$

$frac{sqrt{3}}{2}$

$frac{sqrt{2}}{2}$

$frac{1}{2}$

$0$

$-frac{1}{2}$

$-frac{sqrt{2}}{2}$

$-frac{sqrt{3}}{2}$

$-1$

$-frac{sqrt{3}}{2}$

$-frac{sqrt{2}}{2}$

$-frac{1}{2}$

$0$

$frac{1}{2}$

$frac{sqrt{2}}{2}$

$frac{sqrt{3}}{2}$

$1$

$ an A$

$0$

$frac{sqrt{3}}{3}$

$1$

$sqrt{3}$

$-$

$-sqrt{3}$

$-1$

$-frac{sqrt{3}}{3}$

$0$

$frac{sqrt{3}}{3}$

$1$

$sqrt{3}$

$-$

$-sqrt{3}$

$-1$

$-frac{sqrt{3}}{3}$

$0$

$cot A$

$-$

$sqrt{3}$

$1$

$frac{sqrt{3}}{3}$

$0$

$-frac{sqrt{3}}{3}$

$-1$

$-sqrt{3}$

$-$

$sqrt{3}$

$1$

$frac{sqrt{3}}{3}$

$0$

$-frac{sqrt{3}}{3}$

$-1$

$-sqrt{3}$

$-$

The easiest way to remember the basic values of sin and cosat the angles of 0°, 30°, 60°, 90°:sin(<0, 30, 45, 60, 90>) = cos(<90, 60, 45, 30, 0>) = sqrt(<0, 1, 2, 3, 4>/4)

Basic Trigonometric Identities

For every angle A corresponds exactly one point P(cos(A),sin(A)) on the unit circle.

cos2(A) + sin2(A) = 1

If A + B = 180° then:
sin(A) = sin(B)cos(A) = -cos(B)tan(A) = -tan(B)cot(A) = -cot(B)

If A + B = 90° then:
sin(A) = cos(B)cos(A) = sin(B)tan(A) = cot(B)cot(A) = tan(B)

	$-A$	$90^circ – A$	$90^circ + A$	$180^circ – A$
$ extrm{ sin }$	$- extrm{ sin }A$	$ extrm{ cos }A$	$ extrm{ cos }A$	$ extrm{ sin }A$
$ extrm{ cos }$	$ extrm{ cos }A$	$ extrm{ sin }A$	$- extrm{ sin}A$	$- extrm{ cos }A$
$ extrm{ tan }$	$- extrm{ tan }A$	$ extrm{ cot }A$	$- extrm{ cot }A$	$- extrm{ tan } A$
$ extrm{ cot }$	$- extrm{ cot }A$	$ extrm{ tan }A$	$- extrm{ tan }A$	$- extrm{ cot }A$

Trigonometric Formulas

Half-Angle Formulas

$sinfrac{A}{2}=pmsqrt{frac{1-cos A}{2}}$+ if $frac{A}{2}$ lies in quadrant | or ||- if $frac{A}{2}$ lies in quadrant ||| or |V

$cosfrac{A}{2}=pmsqrt{frac{1+cos A}{2}}$+ if $frac{A}{2}$ lies in quadrant | or |V – if $frac{A}{2}$ lies in quadrant || or |||

$ anfrac{A}{2}=pmsqrt{frac{1-cos A}{1+cos A}}$+ if $frac{A}{2}$ lies in quadrant | or |||- if $frac{A}{2}$ lies in quadrant || or |V

$cotfrac{A}{2}=pmsqrt{frac{1+cos A}{1-cos A}}$+ if $frac{A}{2}$ lies in quadrant | or |||- if $frac{A}{2}$ lies in quadrant || or |V

$ anfrac{A}{2} = frac{sin A}{1+cos A} = frac{1-cos A}{sin A}=csc A-cot A$

$cotfrac{A}{2} = frac{sin A}{1-cos A} = frac{1+cos A}{sin A}=csc A+cot A$

Double and Triple Angle Formulas

$sin(2A) = 2sin(A)cdot cos(A)$

$cos(2A) = cos^2(A) – sin^2(A) = 2cos^2(A) – 1 = 1 – 2sin^2(A)$

$ an(2A) = frac{2 an(A)}{1- an^2(A)}$

$cos(2A) = frac{1 – an^2(A)}{1 + an^2(A)}$

$sin(2A) = frac{2 an(A)}{1 + an^2(A)}$

$sin3A = 3sin A – 4 sin^3A$

$cos3A = 4cos^3A – 3 cos A$

$ an3A=frac{3 an A – an^3A}{1-3 an^2A}$

$cot3A=frac{cot^3A-3cot A}{3cot^2A-1}$

$sin4A = 4cos^3Acdot sin A – 4cos Acdot sin^3A$

$cos4A = cos^4A – 6cos^2Acdot sin^2A + sin^4A$

$ an4A=frac{4 an A – 4 an^3A}{1-6 an^2A+ an^4A}$

$cot4A=frac{cot^4A-6cot^2A+1}{4cot^3A-4cot A}$

Power-Reducing Formulas

$sin^2(A)=frac{1 – cos(2A)}{2}$

$sin^3(A)=frac{3sin A – sin(3A)}{4}$

$sin^4(A)=frac{cos(4A) – 4cos(2A) + 3}{8}$

$cos^2(A) = frac{1 + cos(2A)}{2}$

$cos^3(A)=frac{3cos A + cos(3A)}{4}$

$cos^4(A)=frac{4cos(2A) + cos(4A) + 3}{8}$

Sum and Difference of Angles

$sin(A + B) = sin(A)cdot cos(B) + cos(A)cdot sin(B)$

$sin(A – B) = sin(A)cdot cos(B) – cos(A)cdot sin(B)$

$cos(A + B) = cos(A)cdot cos(B) – sin(A)cdot sin(B)$

$cos(A – B) = cos(A)cdot cos(B) + sin(A)cdot sin(B)$

$ an(A + B) = frac{sin(A + B)}{cos(A + B)}=frac{sin(A)cdot cos(B) + cos(A)cdot sin(B)}{cos(A)cdot cos(B) – sin(A)cdot sin(B)}$

$ an(A + B) = frac{ an(A) + an(B)}{1 – an(A)cdot an(B)}$

$cot(A pm B) = frac{cot(B)cot(A)mp 1}{cot(B)pm cot(A)}=frac{1mp an(A) an(B)}{ an(A)pm an(B)}$

$sin(A + B + C) = sin Acdotcos Bcdotcos C + cos Acdotsin Bcdotcos C + cos Acdotcos Bcdotsin C – sin Acdotsin Bcdotsin C$

$cos(A + B + C) = cos Acdotcos Bcdotcos C – sin Acdotsin Bcdotcos C – sin Acdotcos Bcdotsin C $$- sin Acdotcos B cdotsin C – cos A cdot sin Bcdot sin C$

$ an(A + B + C) = frac{ an A + an B + an C – an Acdot an B cdot an C}{1 – an A cdot an B – an Bcdot an C – an Acdot an C}$

Sum and Difference of Trigonometric Functions

$ extrm{ sin } A + extrm{ sin }B = 2 extrm{ sin }frac{A + B}{2} extrm{ cos }frac{A – B}{2}$

$ extrm{ sin } A – extrm{ sin }B = 2 extrm{ sin }frac{A – B}{2} extrm{ cos }frac{A + B}{2}$

$ extrm{ cos } A + extrm{ cos }B = 2 extrm{ cos }frac{A + B}{2} extrm{ cos }frac{A – B}{2}$

$ extrm{ cos } A – extrm{ cos }B = -2 extrm{ sin }frac{A + B}{2} extrm{ sin }frac{A – B}{2}$

$ an A + an B = frac{sin(A+B)}{cos A cdotcos B}$

$ an A – an B = frac{sin(A-B)}{cos Acdotcos B}$

$cot A + cot B = frac{sin(A+B)}{sin Acdotsin B}$

$cot A – cot B = frac{-sin(A-B)}{sin Acdotsin B}$

Multiplication of 2 Trigonometric Functions

$ extrm{ sin }A extrm{ sin }B = frac{1}{2} ( extrm{ cos }(A – B) – extrm{ cos }(A + B))$

$ extrm{ cos }A extrm{ cos }B = frac{1}{2} ( extrm{ cos }(A – B) + extrm{ cos }(A + B))$

$ extrm{ sin }A extrm{ cos }B = frac{1}{2} ( extrm{ sin }(A + B) + extrm{ sin }(A – B))$

$ an A cdot an B = frac{ an A+ an B}{cot A+cot B}=-frac{ an A- an B}{cot A-cot B}$

$cot A cdot cot B = frac{cot A+cot B}{ an A+ an B}$

$ an A cdot cot B = frac{ an A+cot B}{cot A+ an B}$

$sin Asin Bsin C = frac{1}{4}ig(sin(A+B-C)+sin(B+C-A)+sin(C+A-B)-sin(A+B+C)ig)$

$cos Acos Bcos C = frac{1}{4}ig(cos(A+B-C)+cos(B+C-A)+cos(C+A-B)+cos(A+B+C)ig)$

$sin Asin Bcos C = frac{1}{4}ig(-cos(A+B-C)+cos(B+C-A)+cos(C+A-B)-cos(A+B+C)ig)$

$sin Acos Bcos C = frac{1}{4}ig(sin(A+B-C)-sin(B+C-A)+sin(C+A-B)+sin(A+B+C)ig)$

Tangent half-angle substitution

$sin A = frac{2 anfrac{A}{2}}{1+ an^2frac{A}{2}}$

$cos A = frac{1- an^2frac{A}{2}}{1+ an^2frac{A}{2}}$

$ an A = frac{2 anfrac{A}{2}}{1- an^2frac{A}{2}}$

$cot A = frac{1- an^2frac{A}{2}}{2 anfrac{A}{2}}$

Other Trigonometric Formulas

$1pmsin A=2sin^2ig(frac{pi}{4}pm frac{A}{2}ig)=2cos^2ig(frac{pi}{4}mp frac{A}{2}ig)$

$frac{1-sin A}{1+sin A} = an^2(frac{pi}{4}-frac{A}{2})$

$frac{1-cos A}{1+cos A} = an^2frac{A}{2}$

$frac{1- an A}{1+ an A} = an(frac{pi}{4}-A)$

$frac{1+ an A}{1- an A} = an(frac{pi}{4}+A)$

$frac{cot A + 1}{cot A – 1} = cot(frac{pi}{4}-A)$

$ an A + cot A = frac{2}{sin2A}$

$ an A – cot A = -2cot2A$

Other resources
Trigonometry in detailsTrigonometry forumPracticeTrigonometry in geometryTrigonometric functions plotter