Cách Xác Định Tâm Đường Tròn Ngoại Tiếp, Đường Tròn Ngoại Tiếp Tam Giác Là Gì

Tra cứu điểm thi tốt nghiệp thpt quốc gia 2021 chính xác nhất tại link sau đây: https://khoayduochanoi.com/link-tra-cuu-diem-thi-thpt-quoc-gia-2021-2022-chuan-nhat/

Trong môn Toán 9, người học cần nắm được ĐT, đặc biệt là tâm đường tròn ngoại tiếp tam giác. Từ sự quan trọng của lý thuyết này, Tuvantuyensinh hiểu được điều đó nên đã tổng hợp những kiến ​​thức bổ ích cho người học. ĐT ngoại tiếp TG là gì? Công thức tính bán kính, tìm được tâm ĐT ngoại tiếp … sẽ có trong bài viết dưới đây

1. Khái niệm tâm đường tròn ngoại tiếp tam giác

– ĐT ngoại tiếp TG là một ĐT được vẽ mà nó đi qua 3 đỉnh của TG đã cho sẵn. Nói cách khác, TG nằm trong ĐT hay nội tiếp ĐT

– Ví dụ về ĐT ngoại tiếp TG:

Đường phân giác trung trực của đoạn thẳng EG là đường thẳng đi qua trung điểm M của EG, vuông góc với EG. Mọi điểm I trên đoạn thẳng EG đều có IE = IG.

Đang xem: Tâm đường tròn ngoại tiếp

Ba đường phân giác vuông góc đồng quy tại một điểm. Gọi I là giao điểm của ba đường trung trực của TG ABC thì ta có IA = IB = IC, I là tâm đường tròn ngoại tiếp tam giác ABC. ĐT ngoại tiếp TG là ĐT đi qua 3 đỉnh của TG đã cho.

– Cách vẽ tâm đường tròn ngoại tiếp tam giác

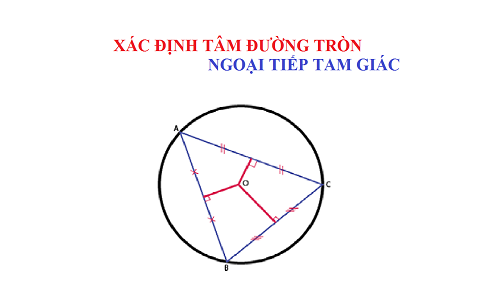
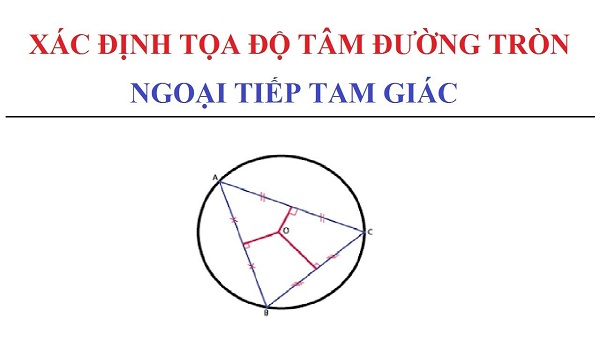
Công thức Circumcenter

P (X, Y) = <(x 1 sin 2A + x 2 sin 2B + x 3 sin 2C) / (sin 2A + sin 2B + sin 2C), (y 1 sin 2A + y 2 sin 2B + y 3 sin 2C) / (sin 2A + sin 2B + sin 2C)>

Đây,

A (x 1 , y 1 ), B (x 2 , y 2 ) và C (x 3 , y 3 ) là các đỉnh của tam giác và A, B, C là các góc tương ứng của chúng.

Phương pháp tính đường tròn tâm của tam giác

Các bước để tìm đường tròn ngoại tiếp tam giác là:

Tính trung điểm của các tọa độ đã cho, tức là trung điểm của AB, AC và BCTính độ dốc của một đường cụ thểBằng cách sử dụng trung điểm và hệ số góc, hãy tìm phương trình của đường thẳng (yy 1 ) = m (xx 1 )Tìm ra phương trình của đường thẳng kia theo cách tương tựGiải phương trình hai đường phân giác bằng cách tìm giao điểmGiao điểm được tính toán sẽ là đường tròn của tam giác đã cho

Tìm đường tròn bằng phương trình tuyến tính

Đường tròn cũng có thể được tính bằng cách lập phương trình tuyến tính sử dụng công thức khoảng cách. Chúng ta hãy lấy (X, Y) là tọa độ của đường tròn ngoại tiếp. Theo tính chất của đường tròn, khoảng cách của (X, Y) từ mỗi đỉnh của một tam giác sẽ như nhau.

Giả sử rằng D1 là khoảng cách giữa đỉnh (x 1 , y 1 ) và đường tròn (X, Y), sau đó công thức được cho bởi,

D 1 = √ <(X − x 1 ) 2 + (Y − y 1 ) 2 >

D 2 = √ <(X − x 2 ) 2 + (Y − y 2 ) 2 >

D 3 = √ <(X − x 3 ) 2 + (Y − y 3 ) 2 >

Bây giờ, vì D 1 = D 2 và D 2 = D 3 , chúng ta nhận được

(X − x 1 ) 2 + (Y − y 1 ) 2 = (X − x 2 ) 2 + (Y − y 2 ) 2

Từ đó thu được hai phương trình tuyến tính. Bằng cách giải các phương trình tuyến tính bằng phương pháp thay thế hoặc loại bỏ, tọa độ của đường tròn có thể thu được.

Xem thêm: Cách Chuyển Tiền Từ Singapore Về Việt Nam Dễ Dàng Nhất, Gửi Tiền Từ Singapore Về Việt Nam

Thuộc tính của Circumcenter

Một số tính chất của đường tròn ngoại tiếp tam giác như sau:

Đường tròn ngoại tiếp là tâm của đường tròn ngoại tiếpTất cả các đỉnh của một tam giác đều cách đều với đường tròn ngoại tiếpTrong một tam giác có góc nhọn, đường tròn nằm bên trong tam giácTrong một tam giác có góc tù, nó nằm bên ngoài của tam giácĐường tròn nằm ở trung điểm cạnh huyền của tam giác vuông

Làm thế nào để xây dựng hình tròn của một tam giác?

Đường tròn ngoại tiếp của bất kỳ tam giác nào có thể được xây dựng bằng cách vẽ đường phân giác vuông góc của hai cạnh bất kỳ của tam giác đó. Các bước để tạo đường tròn ngoại tiếp là:

Bước 1: Vẽ đường phân giác vuông góc của hai cạnh bất kỳ của tam giác đã cho.Bước 2: Dùng thước kẻ, kéo dài các đường phân giác vuông góc cho đến khi chúng cắt nhau.Bước 3: Đánh dấu giao điểm là P sẽ là đường tròn ngoại tiếp tam giác. Cần lưu ý rằng, ngay cả đường phân giác của cạnh thứ ba cũng sẽ cắt nhau tại P.Xây dựng hình tam giácXây dựng tam giác với chu vi và hai góc của nó

Câu hỏi Ví dụ Sử dụng Công thức Vòng tròn

Câu hỏi: Tìm tọa độ đường tròn ngoại tiếp tam giác ABC với các đỉnh A = (3, 2), B = (1, 4) và C = (5, 4)?

Giải pháp:

Phương pháp 1:

Gọi, (x, y) là tọa độ của đường tròn.

D 1 là khoảng cách từ đường tròn ngoại tiếp đến đỉnh A

D 2 là khoảng cách từ đường tròn ngoại tiếp đến đỉnh B

D 3 là khoảng cách từ đường tròn ngoại tiếp đến đỉnh C

Cho: (x 1 , y 1 ) = (3, 2); (x 2 , y 2 ) = (1, 4) và (x 3 , y 3 ) = (5, 4)

Sử dụng công thức khoảng cách, chúng tôi nhận được

D 1 = √ <(X − x 1 ) 2 + (Y − y 1 ) 2 >

D 2 = √ <(X − x 2 ) 2 + (Y − y 2 ) 2 >

D 3 = √ <(X − x 3 ) 2 + (Y − y 3 ) 2 >

Vì D 1 = D 2 = D 3 .

Xem thêm: Tóm Tắt Văn Bản Buổi Học Cuối Cùng Lớp 6, Tóm Tắt Truyện Buổi Học Cuối Cùng Của Tác Giả An

D 1 = D 2 cho,

(x – 3) 2  + (y – 2) 2  = (x – 1) 2  + (y – 4) 2

⇒ x 2  – 6x + 9 + y 2  + 4 – 4y = x 2  + 1 – 2x + y 2  – 8y + 16

⇒ -6x – 4y + 13 = -2x – 8y + 17

⇒ -4x + 4y = 4

⇒ -x + y = 1 ———– (1)

D 1 = D 3 cho,

(x – 3) 2 + (y – 2) 2  = (x – 5) 2  + (y – 4) 2

⇒ x 2  – 6x + 9 + y 2  + 4 – 4y = x 2  + y 2  – 10x – 8y + 25 + 16

⇒ -6x – 4y + 13 = -10x – 8y + 41

⇒ 4x + 4y = 28

Hoặc, x + y = 7 ————– (2)

Bằng cách giải phương trình (1) và (2), chúng ta nhận được

2y = 8

Hoặc, y = 4

Bây giờ, thay y = 4 vào phương trình (1),

⇒ -x + 4 = 1

⇒ -x = 1 – 4

⇒ -x = -3

Hoặc, x = 3

Do đó, đường tròn ngoại tiếp tam giác là (x, y) = (3, 4)

Phương pháp 2:

Các điểm đã cho là,

A = (3, 2),

B = (1, 4),

C = (5, 4)

Để tìm đường tròn, chúng ta phải giải phương trình hai đường phân giác bất kỳ và tìm giao điểm.